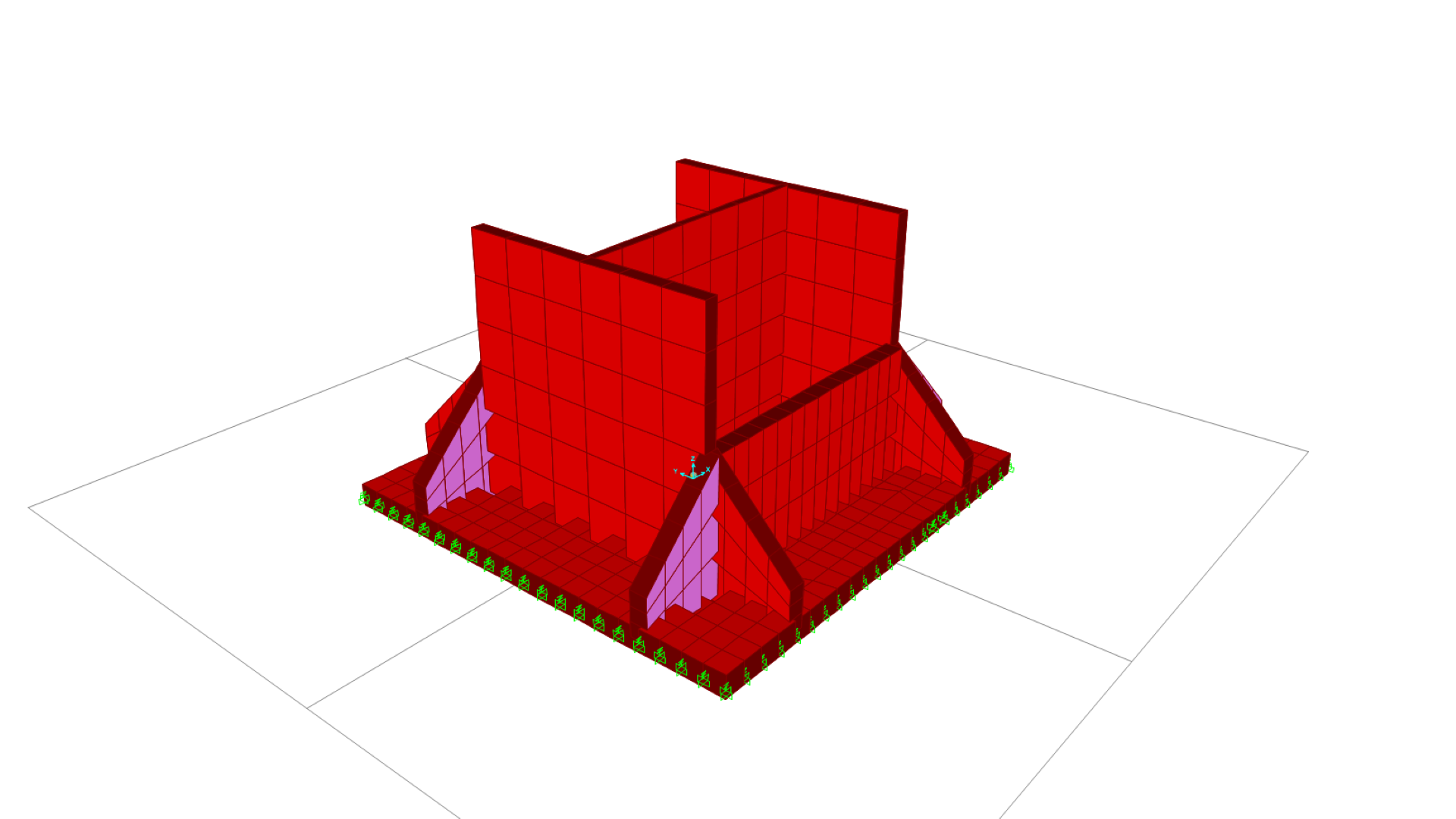
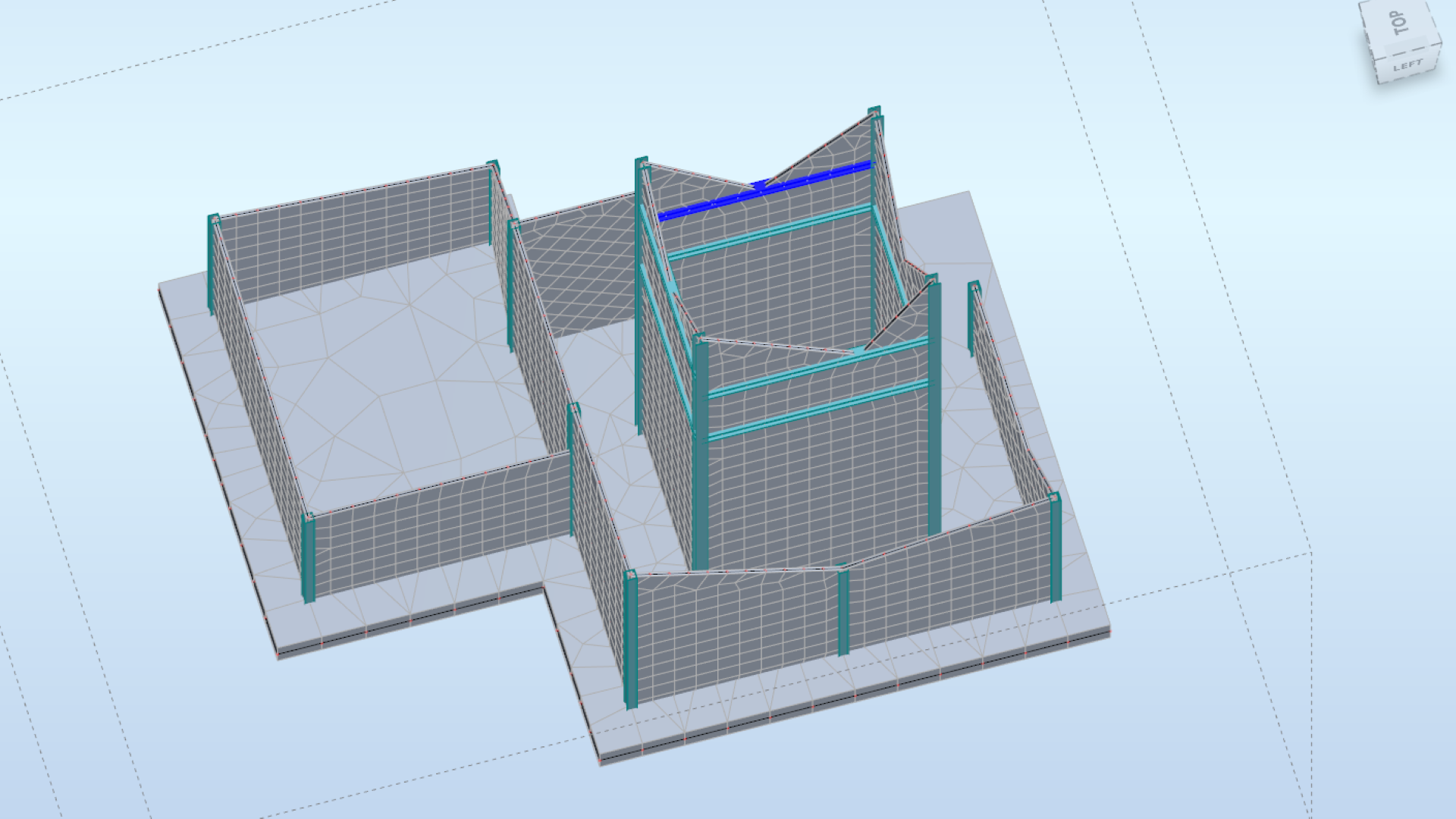
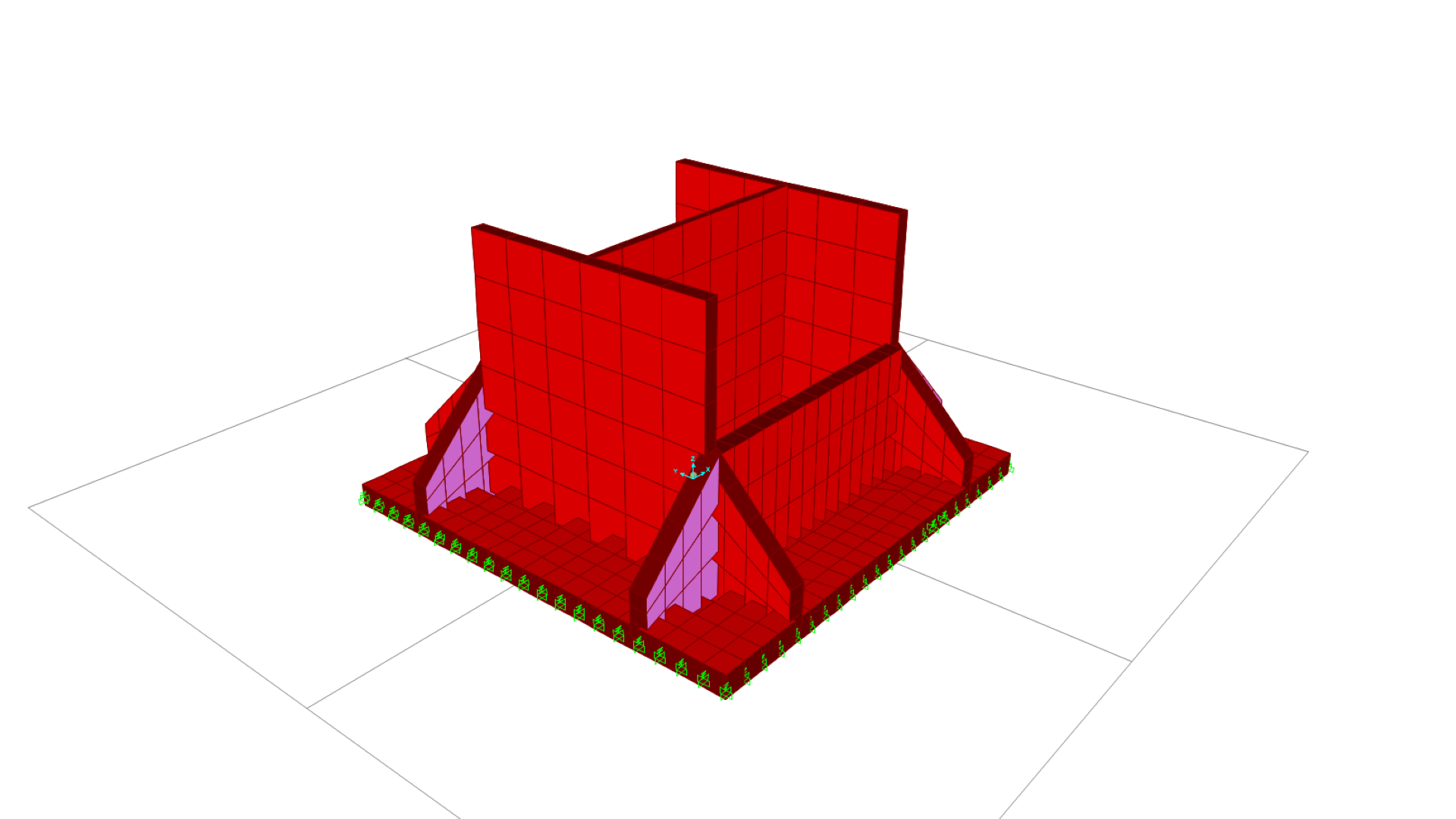
The Finite Element Method (FEM) is a numerical calculation technique widely used in engineering, architecture and construction. It is a particularly useful method for analysing complex structures and solving problems that were previously considered unsolvable due to their high computational demands. One such issue, for example, is the strength of materials.
The FEM technique is applied by dividing an object that is difficult to analyse, in our case, a building or a structure, into small parts or “finite elements“. Based on established boundary conditions, the geometry and material properties are defined and a mesh is created. The finer the mesh, the better the results, but also the longer the time required for computational analysis.
The method deals with solving differential equations with N equations and N unknowns, in the context of architecture and construction, and provides the exact solution (for both deformations and stresses) at the nodes generated between the meshes. For the points outside the nodes, interpolation is applied in order to obtain an approximate solution.
Thanks to FEM calculation and analysis, the need for prototype testing is reduced, project development time is reduced and a more detailed and accurate structural analysis is achieved. It is a valuable tool in engineering, architecture and construction to solve complex problems efficiently.
By Alberto Lopez, Senior Structural Engineer in the Architecture Department of Amusement Logic