In a previous article, we presented the particularities of a phenomenon known as water hammer that occurs in hydraulic networks in general, and those of water parks in particular. In this new investigation of the same phenomenon, we will differentiate between fast and slow water hammer, depending on the closing time of the shut-off valve, and we will present various formulations for calculating the overpressure associated with each of these types. Finally, we will present the specific cases in which water hammer occurs in the hydraulic installations of water parks, and the measures available to mitigate it.
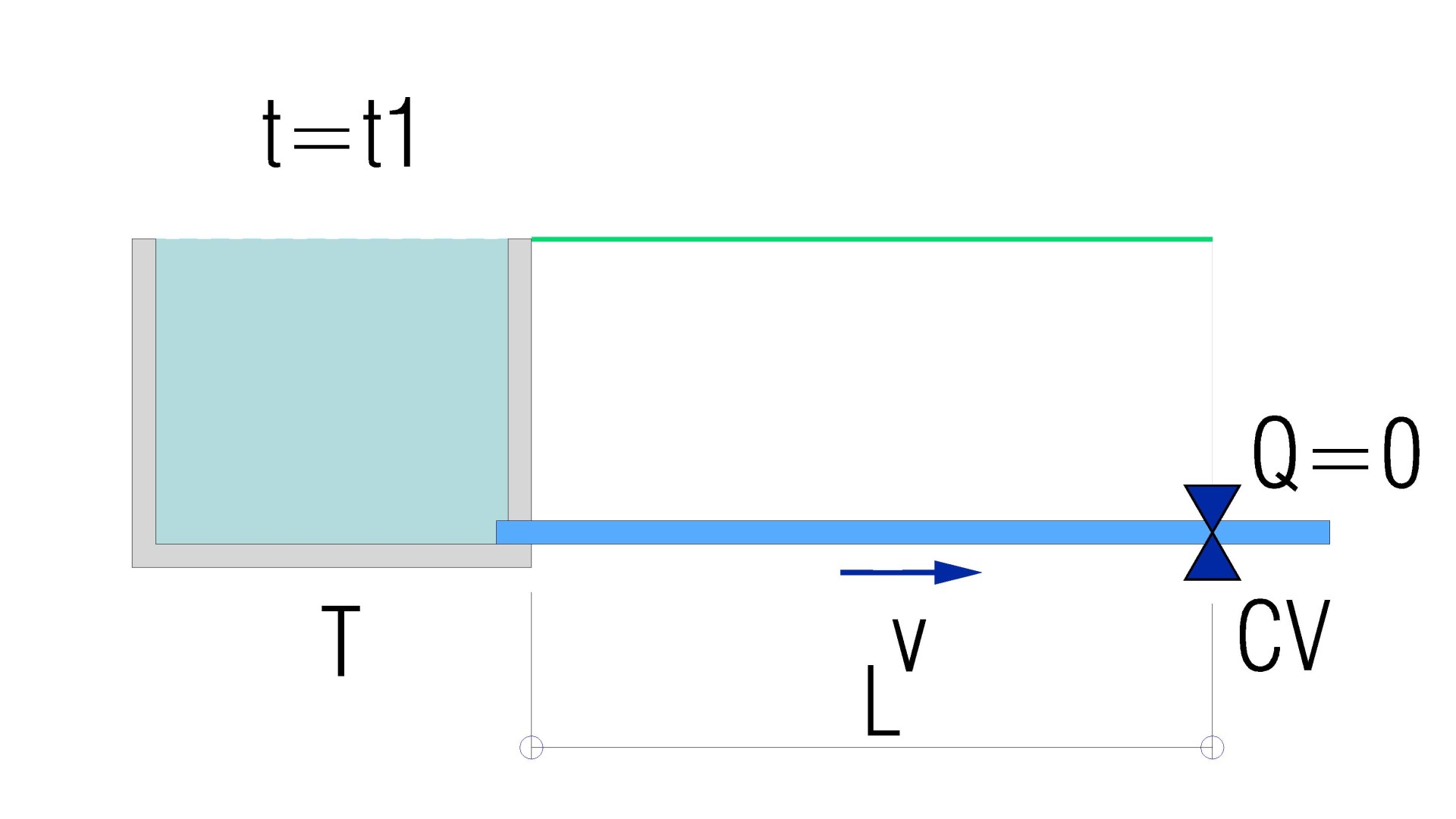
In the context of the same example used in the previous article, we determine that the closing time (Tc) corresponds to the duration of the flow cut-off manoeuvre in the pipe. Likewise, the time taken for the overpressure wave (of velocity a) to travel through the pipe (of length L), from the shut-off valve (CV) to the tank (T), we will call it L/a. Consequently, the reflected wave from the tank will reach the valve in time 2-L/a.
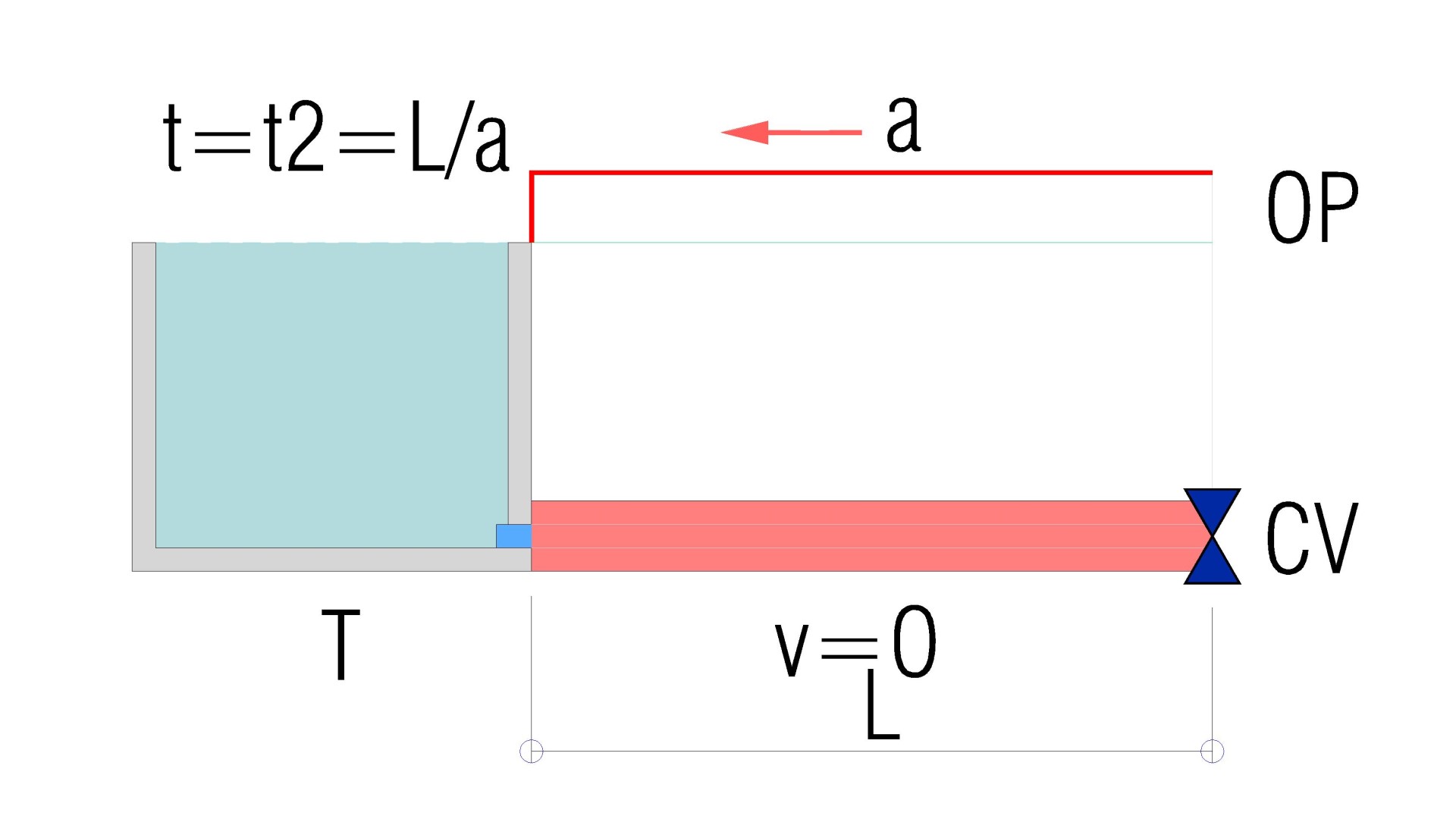
The image shows the instant t2 = L/a, the moment when the overpressure wave reaches the tank.
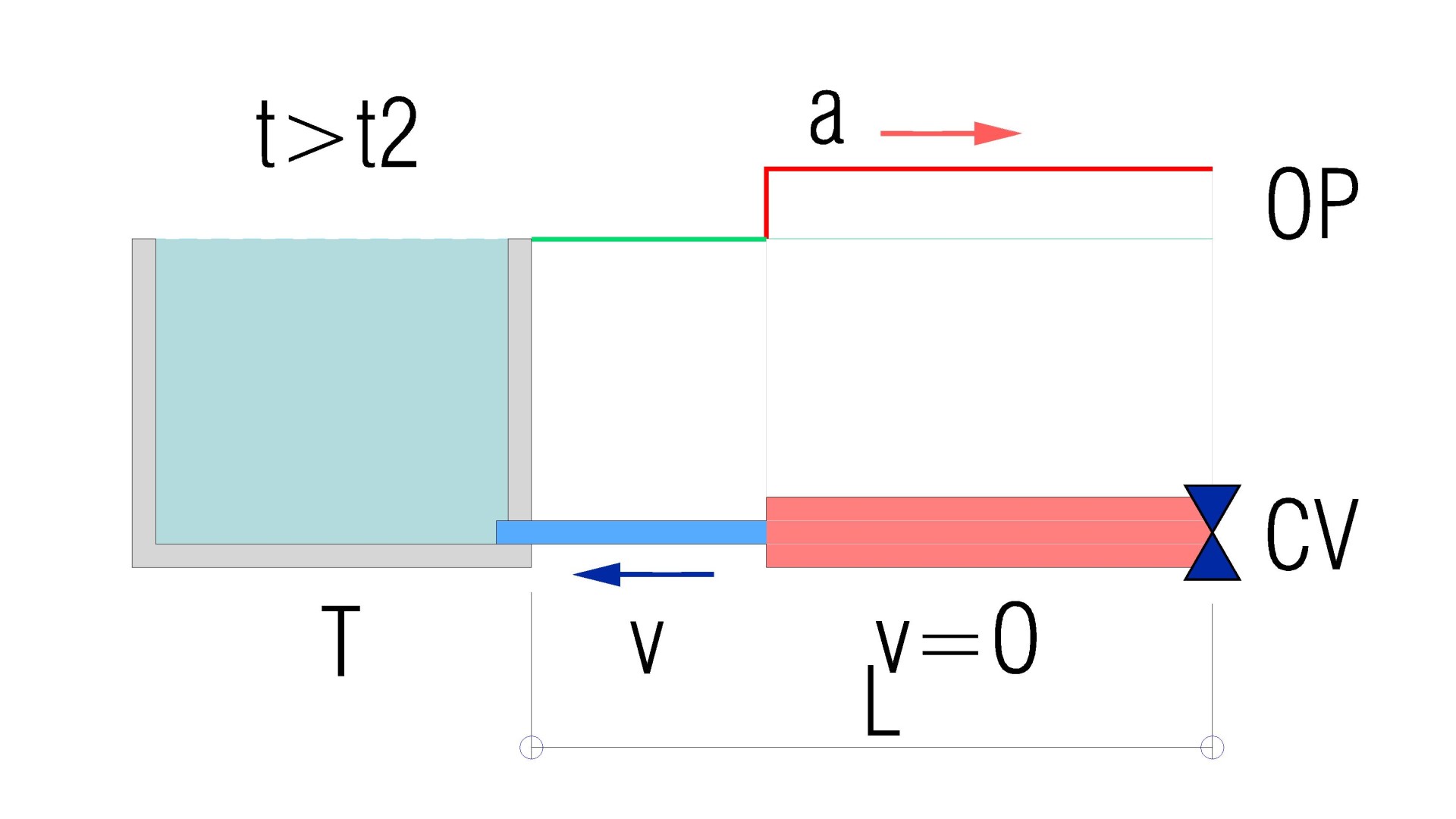
The pressure wave is then reflected and returns to the shut-off valve.
Therefore, it is at the instant t3 = 2-L/a, when the pressure wave reaches the shut-off valve.
When the closing is fast or, in other words, Tc < 2-L/a, the overpressure wave reaches the valve when it is already completely closed. In this case, the overpressure (OP) is calculated with Allievi’s formula, as follows:
OP = a-v/g
Where:
a: velocity of the wave
v: fluid velocity
g: acceleration of gravity
Therefore, in fast closures, the overpressure is independent of the closing time, and is equivalent to that which would occur if the closure were instantaneous, or Tc ≈ 0.
When the closure is slow, or Tc > 2-L/a: in this case, the overpressure wave reaches the valve when it has not yet closed completely, which means that part of the overpressure is relieved. In this situation, the overpressure is calculated using Michaud’s formula:
OP = 2-L-v/(g-Tc)
As can be seen, in slow closing, the overpressure is inversely proportional to the closing time of the valve. Therefore, the longer the closing time, the lower the overpressure in the pipe due to water hammer.

Hydraulic installations in water parks, with large pumping units from which water is pumped to water slides and other attractions, can be subject to water hammer during the pump stop manoeuvre. In this case, a negative pressure wave front is produced and, as a result, water hammer is triggered in its reverse phase. To mitigate this effect, it must be ensured that the pump stop time (equivalent to the valve closure time, or Tc, described above) is longer than the travel time of the 2-L/a pressure wave. We will therefore be in the slow closing option (slow pump stop) and, therefore, the overpressure produced in the pipe will be ostensibly lower. It goes without saying that the slower the stop, the lower the overpressure will be.
In practice, in order to avoid water hammer, pumps in water parks are often installed with frequency converters or soft starters. These devices ensure that the pumps stop slowly enough so that the overpressure in the pipeline is negligible.
By Luis Llor, Senior Hydraulic Engineer in Amusement Logic’s Architecture Dept.






