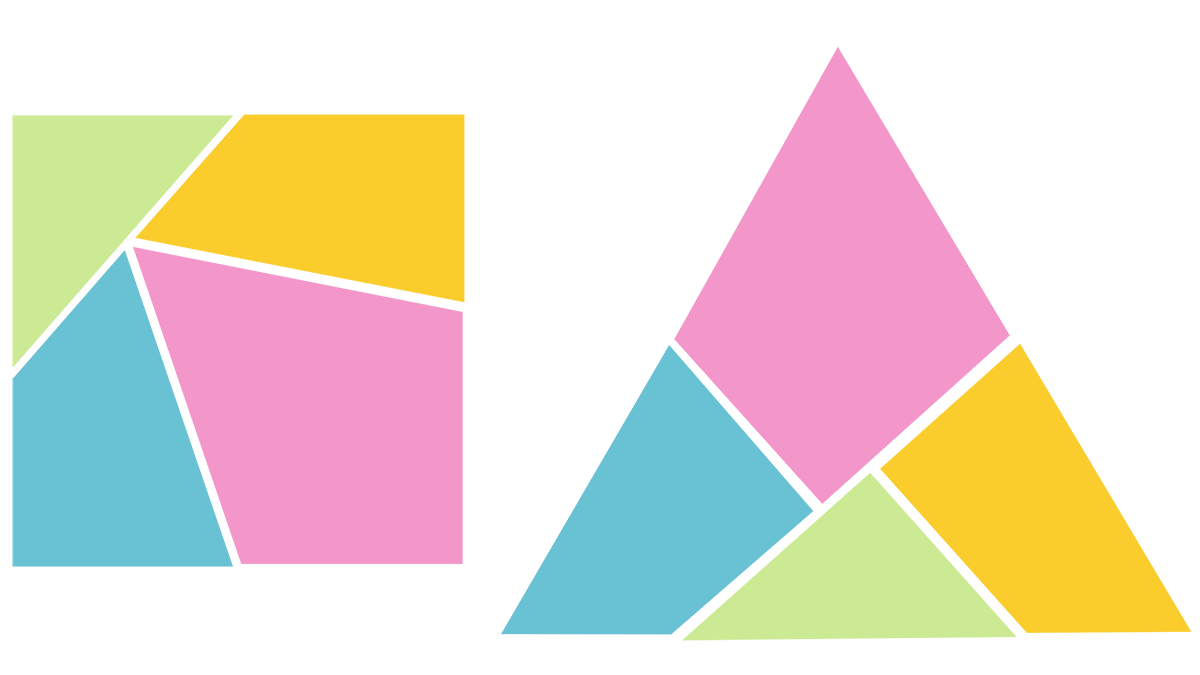In 1902, the English mathematician Henry Ernest Dudeney (1857-1930) posed a seemingly simple challenge in his puzzle column in the Sunday paper Weekly Dispatch—known as the Sunday Dispatch from 1928 to 1961, the year it merged with the Sunday Express—but one that concealed a fascinating complexity: how to divide an equilateral triangle into the smallest possible number of pieces so that, when rearranged (through translation and rotation only, without superposition), they form a perfect square?
A reader named Charles William McElroy proposed an ingenious solution using only four pieces connected at their vertices and hinged, a sort of mechanical puzzle that allowed the triangle to be transformed into a square with a simple twist. For the past 122 years, no one has achieved the same result with fewer than four pieces, although there has never been any evidence that it could be achieved.
If there were any doubts, they were dispelled in December 2024, when mathematicians Tonan Kamata and Ryuhei Uehara of the Advanced Institute of Science and Technology in Japan, and Erik D. Demaine of the Massachusetts Institute of Technology in the United States, showed that it is not possible to solve the problem with fewer than four pieces. Therefore, the solution given by McElroy and Dudeney more than a century ago is “optimal”—or, to put it another way, a more efficient solution is impossible.
To solve the geometric enigma, Kamata and his fellow mathematicians reduced it to a graph theory problem. That way, instead of attempting infinite combinations of geometric cuts, they limited the problem to one of analysing possible dissections as possible graphs. Incidentally, a graph is a mathematical structure made up of vertices—also known as nodes or points—connected by edges—also called arcs, links, or lines. Graph theory is therefore the branch of mathematics that studies graphs. But back to the geometric puzzle: indeed, each cut of the initial equilateral triangle is represented as an edge, and each intersection point as a vertex. With this, they managed to classify all possible variations into manageable categories and reduced an infinite problem to a finite set of cases. You already know the result.
Beyond its theoretical value, this discovery has implications in fields as diverse as design, architecture, and even mathematical pedagogy. To cite just one example, the London design and architecture studio DHaus translated the Dudeney puzzle—also known as the “Dudeney dissection” or the “haberdasher’s problem,” the latter appellation coming from Dudeney’s own presentation of it as puzzle number 26 in The Canterbury Puzzles (1907)—into the form of a haberdasher’s challenge to his interlocutors: to cut a piece of cloth in the shape of an equilateral triangle to form that perfect square. The DHaus studio, we mentioned, translated this geometric play into the design of a table and a house with moving parts.
You see, seemingly simple problems can hide unsuspected depths. In any case, the next time you see a triangle or a square, perhaps you’ll remember that, behind their seemingly static shape, lie unexpected connections, surprising transformations, and, above all, the eternal elegance of mathematics.
Sources: Arxiv.org, Scientific American, Wolfram MathWorld, Gutenberg.org, Wikipedia.
Images: DHaus 1, DHaus 2, Wikipedia.